Расчет балки

Теория по методу начальных параметров

Возьмем консольную балку, нагруженную сосредоточенной силой, моментом, а также распределенной нагрузкой. Таким образом, зададимся такой расчетной схемой, где присутствуют все виды нагрузок, тем самым, охватим всю теоретическую часть по максимуму. Обозначим опорные реакции в жесткой заделке, возникающие под действием внешней нагрузки:

Выбор базы и обозначение системы координат

Для балки выберем базу с левой стороны, от которой будем отсчитывать расстояния до приложения сил, моментов, начала и конца распределенной нагрузки. Базу обозначим буквой O и проведем через нее систему координат:

Базу традиционно выбирают с левого краю балки, но можно выбрать ее и справа. Тогда в уравнении будут противоположные знаки, это может пригодиться в некоторых случаях, упростит немного решение. Понимание, когда принимать базу слева или справа, придет с опытом решения задач на метод начальных параметров.

Универсальное уравнение прогибов для балки

После введения базы, системы координат и обозначении расстояний а, б, в, г записываем универсальную формулу, с помощью которой, будем рассчитывать прогиб балки (вертикальное перемещение сечения K, находящегося на свободном торце балки): Теперь поговорим об этой формуле, проанализируем так сказать:

• E – модуль упругости;
• I – момент инерции;
• Vk – прогиб сечения K;
• VO – прогиб сечения O;
• θO – угол поворота сечения О.

Итак, изучаем эту формулу с лева направо. В левой части уравнения обознается искомый прогиб, в нашем случае Vk, который дополнительно умножается на жесткость балки — EI:В уравнении всегда учитывается прогиб сечения балки, совпадающего с нашей базой EIVO:

Также всегда учитывается угол поворота сечения совпадающего с выбранной базой. Причем, произведение EIθO всегда умножается на расстояние от базы до сечения, прогиб которого рассчитывается, в нашем примере — это расстояние г.

Следующие компоненты этого уравнения учитывают всю нагрузку находящуюся слева от рассматриваемого сечения. В скобках расстояния от базы до сечения отнимаются расстояния от базы до соответствующей силы или момента, начала или конца распределенной нагрузки.

Скобка, в случае с сосредоточенными силами, возводится в 3 степень и делится на 6. Если сила смотрит вверх, то считаем ее положительной, если вниз, то в уравнении она записывается с минусом:

В случае с моментами, скоба возводится во 2 степень и делится на 2. Знак у момента будет положительный, когда он направлен почасовой стрелке и отрицательным, соответственно, когда против часовой стрелки.

Учет распределенной нагрузки

Теперь поговорим о распределенной нагрузке. Как уже говорилось, в уравнении метода начальных параметров должно учитываться начало и конец распределенной нагрузки, но конец ее совпадает с сечением, прогиб которого мы хотим вычислить, поэтому в уравнение попадает только ее начало.

Для распределенной нагрузки скобочка возводится в 4 степень и делится на 24. Правило знаков такое же, как и для сосредоточенных сил:

Граничные условия

Чтобы решить уравнение нам понадобятся еще кое-какие данные. С первого взгляда в уравнении у нас наблюдается три неизвестных: VK, VO и θO. Но кое-что мы можем почерпнуть из самой схемы. Мы знаем, в жесткой заделке не может быть никаких прогибов, и ни каких поворотов, то есть VO=0 и θO=0, это и есть так называемые начальные параметры или их еще называют граничными условиями. Теперь, если бы у нас была реальная задача, мы бы подставили все численные данные и нашли перемещение сечения K.

Чуть не забыл про еще одну величину, которую часто требуется определять методом начальных параметров. Как известно, при изгибе, поперечные сечения балок помимо того, что перемещаются вертикально (прогибаются) так еще и поворачиваются на какой-то угол. Углы поворота и прогибы поперечных сечений связаны дифференциальной зависимостью.

Если продифференцировать уравнение, которое мы получили для прогиба поперечного сечения K, то получим уравнение угла поворота этого сечения:

Необходимые пояснения к расчетам

• Высота и ширина определяют площадь сечения и механическую прочность балки.
• Материал древесины: сосна, ель или лиственница – характеризует прочность балок, их стойкость к прогибам и излому, другие особые эксплуатационные свойства. Обычно отдают предпочтение сосновым балкам. Изделия из лиственницы применяют для помещений с влажной средой (бань, саун и т.п.), а балки из ели используют при строительстве недорогих дачных домов.
• Сорт древесины влияет на качество балок (по мере увеличения сорта качество ухудшается).
  • 1 сорт. На каждом однометровом участке бруса с любой стороны могут быть здоровые сучки размером 1/4 ширины (пластевые и ребровые), размером 1/3 ширины (кромочные). Могут быть и загнившие сучки, но их количество не должно превышать половины здоровых. Также нужно учитывать, что суммарные размеры всех сучков на участке в 0,2 м должны быть меньше предельного размера по ширине. Последнее касается всех сортов, когда речь идет о несущей балочной конструкции. Возможно наличие пластевых трещин размером 1/4 ширины (1/6, если они выходят на торец). Длина сквозных трещин ограничивается 150 мм, брус первого сорта может иметь торцевые трещины размером до 1/4 ширины. Из пороков древесины допускаются: наклон волокон, крень (не более 1/5 площади стороны бруса), не более 2 кармашков, односторонняя прорость (не более 1/30 по длине или 1/10 — по толщине или ширине). Брус 1 сорта может быть поражен грибком, но не более 10% площади пиломатериала, гниль не допускается. Может быть неглубокая червоточина на обзольных частях. Обобщая вышесказанное: внешний вид такого бруса не должен вызывать какие-либо подозрения.
  • 2 сорт. Такой брус может иметь здоровые сучки размером 1/3 ширины(пластевые и ребровые), размером 1/2 ширины (кромочные). По загнившим сучкам требования, как и для 1 сорта. Материал может иметь глубокие трещины длиной 1/3 длины бруса. Максимальная длина сквозных трещин не должна превышать 200 мм, могут быть трещины на торцах размером до 1/3 от ширины. Допускается: наклон волокон, крень, 4 кармашка на 1 м., прорость (не более 1/10 по длине или 1/5 – по толщине или ширине), рак (протяжением до 1/5 от длины, но не больше 1 м). Древесина может быть поражена грибком, но не более 20% площади материала. Гниль не допускается, но может быть до двух червоточин на 1 м. участке. Обобщим: сорт 2 имеет пограничные свойства между 1 и 3, в целом оставляет положительные впечатления при визуальном осмотре.
  • 3 сорт. Тут допуски по порокам больше: брус может иметь сучки размером 1/2 ширины. Пластевые трещины могут достигать 1/2 длины пиломатериала, допускаются торцевые трещины размером 1/2 от ширины. Для 3 сорта допускается наклон волокон, крень, кармашки, сердцевина и двойная сердцевинаы, прорость (не более 1/10 по длине или 1/4 — по толщине или ширине), 1/3 длины может быть поражена раком, грибком, но гнили не допускаются. Максимальное количество червоточин — 3 шт. на метр. Обобщая: 3 сорт даже невооруженным глазом выделяется не самым лучшим качеством. Но это не делает его непригодным для изготовления перекрытий по балкам.Подробнее про сорта читайте ГОСТ 8486-86 Пиломатериалы хвойных пород. Технические условия;
• Пролет – расстояние между стенами, поперек которых укладываются балки. Чем он больше, тем выше требования к несущей конструкции;
• Шаг балок определяет частоту их укладки и во многом влияет на жесткость перекрытия;
• Коэффициент надежности вводится для обеспечения гарантированного запаса прочности перекрытия. Чем он больше, тем выше запас прочности

Наш онлайн-калькулятор позволит вам рассчитать параметры деревянных балок и подобрать оптимальную конфигурацию перекрытия.

Особенности расчета на прогиб

Расчет на прогиб проводится обязательно для любых перекрытий. Крайне важен точный расчет данного показателя при значительных внешних нагрузках. Сложные формулы в данном случае использовать необязательно. Если использовать соответствующие коэффициенты, то вычисления можно свести к простым схемам:

1. Стержень, который опирается на одну жесткую и одну шарнирную опору, и воспринимает сосредоточенную нагрузку.
2. Стержень, который опирается на жесткую и шарнирную опору, и при этом на него действует распределенное нагружение.
3. Варианты нагружения консольного стержня, который закреплен жестко.
4. Действие на конструкцию сложной нагрузки.

Применение этого метода вычисления прогиба позволяет не учитывать материал. Поэтому на расчеты не влияют значения его основных характеристик.

Расчет статически неопределимой балки

Поскольку данная балка является статически неопределимой, для нее нельзя определить внутренние усилия и реакции опор только методами статики (с помощью уравнений равновесия).

Как правило, для таких случаев сначала следует раскрыть статическую неопределимость, используя один из методов:

• метод сил
• метод уравнения трех моментов
• метод интегрирования дифференциального уравнения изгиба

При раскрытии статической неопределимости определяются некоторые параметры (реакции опор либо опорные моменты), имея которые дальнейший расчет уже возможен с помощью уравнений равновесия.

Будем считать, что статическая неопределимость раскрыта и эпюры уже построены

Записываем уравнения поперечных сил и изгибающих моментов на
участках балки
, используя метод сечений

На участке AB: (0 ≤ z₁ ≤ 2 м )

Q(z₁) = + R_A = + 3.074 = 3.074 кН

M(z₁) = + R_A · z = + 3.074 · z

M(0) = 0 кНм

M(2) = 6.149 кНм

На участке BC: (2 ≤ z₂ ≤ 3 м )

Q(z₂) = + R_A — P — q₁·(z — 2) = + 3.074 — 12 — 5·(z — 2)

Q(2) = -8.926 кН

Q(3) = -13.926 кН

M(z₂) = + R_A · z — P·(z — 2) — q₁·(z — 2)2/2 = + 3.074 · z — 12·(z — 2) — 5·(z — 2)2/2

M(2) = 6.149 кНм

M(3) = -5.277 кНм

На участке CD: (3 ≤ z₃ ≤ 4 м )

Q(z₃) = + R_A + R_C — P — q₁·(z — 2) = + 3.074 + 19.5 — 12 — 5·(z — 2)

Q(3) = 5.57 кН

Q(4) = 0.57 кН

M(z₃) = + R_A · z + R_C · (z — 3) — P·(z — 2) — q₁·(z — 2)2/2 = + 3.074 · z + 19.5 · (z — 3) — 12·(z — 2) — 5·(z — 2)2/2

M(3) = -5.277 кНм

M(4) = -2.207 кНм

На участке DE: (4 ≤ z₄ ≤ 5 м )

Q(z₄) = + R_A + R_C — P — Q₁ = + 3.074 + 19.5 — 12 — 10 = 0.57 кН

M(z₄) = + R_A · z + R_C · (z — 3) — P·(z — 2) — Q₁·(z — 3) = + 3.074 · z + 19.5 · (z — 3) — 12·(z — 2) — 10·(z — 3)

M(4) = -2.207 кНм

M(5) = -1.637 кНм

На участке EF: (5 ≤ z₅ ≤ 6 м )

Q(z₅) = + R_A + R_C — R_E — P — Q₁ = + 3.074 + 19.5 — 6.933 — 12 — 10 = -6.363 кН

M(z₅) = + R_A · z + R_C · (z — 3) — R_E · (z — 5) — P·(z — 2) + M — Q₁·(z — 3) = + 3.074 · z + 19.5 · (z — 3) — 6.933 · (z — 5) — 12·(z — 2) + 8 — 10·(z — 3)

M(5) = 6.363 кНм

M(6) = 0 кНм

Максимальный момент в балке составляет M_max = 6.36 кНм. По этому значению
подбираем сечение балки.

Условие прочности при изгибе σ = M_maxW ≤

Отсюда, минимально необходимый момент сопротивления вычисляем по формуле W_min=M_max

Подбираем двутавровое сечение при допускаемом напряжении = 160 МПа
W_min=6360160 = 39.75 см3
Из сортамента выбираем двутавр №12 с моментом сопротивления W = 58.33 см3 и площадью A = 14.7 см2
Максимальные нормальные напряжения в двутавре составляют
σ_max = M_max/Wx = 6360/58.33 = 109.03 МПа
Максимальные касательные напряжения в двутавре (на центральной оси) составляют
τ_max = Q_max×Sx/b×Ix = 13900×29.66×10-6/0.0048×350×10-8 = 24.54×106 Па = 24.54 МПа
Касательные напряжения на границе полки и стенки составляют
τ_max = Q_max×Sx’/b×Ix = 13900×26.33×10-6/0.0048×350×10-8 = 21.785×106 Па = 21.785 МПа,
где статический момент отсеченной полки составляет
Sx’=b×t×(h-t)/2=6.4×0.73×(12-0.73)/2=26.33 см3.
Эпюры нормальных и касательных напряжений для двутавра:

Подбираем прямоугольное сечение с отношением сторон hb=2
W_min=6360160 = 40 см3
Момент сопротивления прямоугольного сечения
W=b×h26 = b3 × 226 = b3×0.67
b3=400.67=60
Ширина сечения b=3.9 см, Высота сечения h=b×2=3.9×2=7.8 см
Площадь сечения A=b×h=3.9×7.8=30.42 см2
Максимальные нормальные напряжения составляют
σ_max = 6×M_max/b×h2 = 6×6360/3.9×7.82 = 160.83 МПа
Максимальные касательные напряжения для прямоугольника составляют
τ_max = 3Q_max/2A = 3×13900/2×30.42×100 = 6.854 МПа
Эпюры нормальных и касательных напряжений для прямоугольного сечения:

ОБЩИЕ УКАЗАНИЯ

10.1. При расчете строительных конструкций по прогибам (выгибам) и перемещениям должно быть выполнено условие

(25)

где f — прогиб (выгиб) и перемещение элемента конструкции (или конструкции в целом), определяемые с учетом факторов, влияющих на их значения, в соответствии с пп. 1-3 рекомендуемого приложения 6;

fu — предельный прогиб (выгиб) и перемещение, устанавливаемые настоящими нормами.

Расчет необходимо производить исходя из следующих требований:

а) технологических (обеспечение условий нормальной эксплуатации технологического и подъемно-транспортного оборудования, контрольно-измерительных приборов и т.д.);

б) конструктивных (обеспечение целостности примыкающих друг к другу элементов конструкций и их стыков, обеспечение заданных уклонов);

в) физиологических (предотвращение вредных воздействий и ощущений дискомфорта при колебаниях);

г) эстетико-психологических (обеспечение благоприятных впечатлений от внешнего вида конструкций, предотвращение ощущения опасности).

Каждое из указанных требований должно быть выполнено при расчете независимо от других.

Ограничения колебаний конструкций следует устанавливать в соответствии с нормативными документами п. 4 рекомендуемого приложения 6.

10.2. Расчетные ситуации, для которых следует определять прогибы и перемещения, соответствующие им нагрузки, а также требования, касающиеся строительного подъема, приведены в п. 5 рекомендуемого .

10.3. Предельные прогибы элементов конструкций покрытий и перекрытий, ограничиваемые исходя из технологических, конструктивных и физиологических требований, следует отсчитывать от изогнутой оси, соответствующей состоянию элемента в момент приложения нагрузки, от которой вычисляется прогиб, а ограничиваемые исходя из эстетико-психологических требований — от прямой, соединяющей опоры этих элементов (см. также п. 7 рекомендуемого приложения 6).

10.4. Прогибы элементов конструкций не ограничиваются исходя из эстетико-психологических требований, если не ухудшают внешний вид конструкций (например, мембранные покрытия, наклонные козырьки, конструкции с провисающим или приподнятым нижним поясом) или если элементы конструкций скрыты от обзора. Прогибы не ограничиваются исходя из указанных требований и для конструкций перекрытий и покрытий над помещениями с непродолжительным пребыванием людей (например, трансформаторных подстанций, чердаков).

Примечание. Для всех типов покрытий целостность кровельного ковра следует обеспечивать, как правило, конструктивными мероприятиями (например, использованием компенсаторов, созданием неразрезности элементов покрытия), а не повышением жесткости несущих элементов.

10.5. Коэффициент надежности по нагрузке для всех учитываемых нагрузок и коэффициент динамичности для нагрузок от погрузчиков, электрокаров, мостовых и подвесных кранов следует принимать равными единице.

Коэффициенты надежности по ответственности необходимо принимать в соответствии с обязательным приложением 7.

10.6. Для элементов конструкций зданий и сооружений, предельные прогибы и перемещения которых не оговорены настоящим и другими нормативными документами, вертикальные и горизонтальные прогибы и перемещения от постоянных, длительных и кратковременных нагрузок не должны превышать 1/150 пролета или 1/75 вылета консоли.

Основные положения расчетных методик

Современные строительные методики расчета стержневых (балочных) конструкций на прочность и жесткость, дают возможность уже на стадии проектирования определить значение прогиба и сделать заключение о возможности эксплуатации строительной конструкции.Расчет на жесткость позволяет решить вопрос о наибольших деформациях, которые могут возникнуть в строительной конструкции при комплексном действии различного вида нагрузок.

Современные методы расчета, проводимые с использованием специализированных расчетов на электронно-вычислительных машинах, или выполняемые при помощи калькулятора, позволяют определить жесткость и прочность объекта исследований.

Несмотря на формализацию расчетных методик, которые предусматривают использование эмпирических формул, а действие реальных нагрузок учитывается введением поправочных коэффициентов (коэффициенты запаса прочности), комплексный расчет достаточно полно и адекватно оценивает эксплуатационную надежность возведенного сооружения или изготовленного элемента какой-либо машины.

Несмотря на отдельность прочности расчетов и определения жесткости конструкции, обе методики взаимосвязаны, а понятия «жесткость» и «прочность» неразделимы. Однако, в деталях машин, основное разрушение объекта происходит из-за потери прочности, в то время как объекты строительной механики часто непригодны к дальнейшей эксплуатации из значительных пластических деформаций, которые свидетельствуют о низкой жесткости элементов конструкции или объекта в целом.

Сегодня, в дисциплинах «Сопротивление материалов», «Строительная механика» и «Детали машин», приняты два метода расчета на прочность и жесткость:

1. Упрощенный (формальный), при проведении которого в расчетах применяются укрупненные коэффициенты.
2. Уточненный, где используются не только коэффициенты запаса прочности, но и производится расчет контракции по предельным состояниям.

Виды балок

Независимо от того, какой должна быть конструкция, материал для изготовления балок выбирают прочный и надежный. Отличаются они друг от друга лишь по своим параметрам:

1. длине;
2. форме;
3. сечению.

Чаще всего, для изготовления балок используется дерево и металл. Расчет балки на изгиб напрямую зависит от выбранного материала. В данном случае большое значение имеют такие показатели как однородность и структура.

Балки из дерева

Конструкции из дерева используются в одноэтажных домах или небольших домиках. Они отлично подходят как для потолка, так и пола. Для расчета прогиба балки берут следующие величины:

1. Тип материала. Каждое дерево отличается прочностью, твердостью и гибкостью.
2. Геометрические показатели, в которые включается как форма изделия, так и его сечение.
3. Предполагаемые нагрузки, которые будут давить на материал.

На то, как будет изгибаться балка учитывается не только реальное давление, но и все возможные силы воздействия.

Стальные балки

Эти изделия очень сложные не только по сечению, но и по составу. Так как из выливают из нескольких видов металла

Производя расчет нагрузки на балку, необходимо принимать во внимание насколько она жесткая, а так же прочно ли она соединена

Балки из стали используют для строительства многоэтажных домов Источник i0.photo.2gis.com

Конструкция из металла между собой соединяется с помощью:

• сваривания;
• склепывания;
• с помощью соединителей, имеющих резьбу.

Прочные металлические балки используются для строительства домов в несколько этажей. В таких конструкциях вся нагрузка равномерно распределяется по всей балке.

Основы вычислений

Для начала следует понять, что именно требуется рассчитать. Дело в том, что деревянный брус или доска балки под нагрузкой способно изогнуться до определенного предела – эта величина называется пределом прочности – и при дальнейшем увеличении нагрузки сломаться. Под действием нагрузки изогнувшаяся балка может также выскользнуть из креплений. Чтобы избежать этого или хотя бы снизить риск такой неприятности, деревянные балки стараются заделать в кладку дома или прикрепить с помощью кронштейнов, уголков и других видов деталей к деревянной стене дома. Используют также врубку балки в венец стены. Все такие виды фиксации считаются жесткой заделкой.

Вот так примерно выглядит расчетная схема для однопролетной балки, то есть изделие, у которого закреплены только концы. Здесь L – пролет балки, расстояние между опорными точками, Q – распределенная нагрузка, f – величина прогиба.

Основой для расчета предельно допустимого прогиба, как и источником других данных о работе деревянных конструкций, является СП 64.13330.2011. Согласно этому документу, предельный прогиб балки для межэтажных перекрытий не должен превышать 1/250 часть длины пролета.

То есть для балки с длиной 6 м допустимый прогиб составит 24 мм. Если же брать более строгие значения (для штукатурки на потолке и требующих строгой плоскости пола второго этажа напольных покрытий, например, плитки) – 1/350, допустимый прогиб уменьшается до 17 мм.

В целом для вычислений используют формулу f=L/350, при этом длину пролета указывают в миллиметрах.

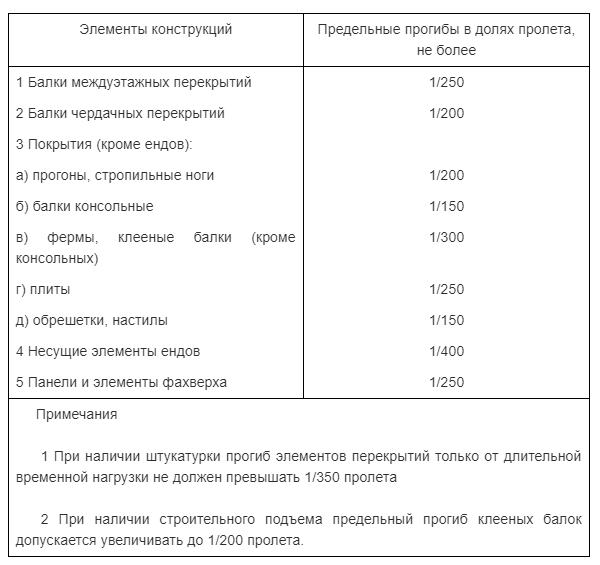
Таблица 1.1. Допустимый прогиб деревянных конструкций.

Соответственно, при расчете балки на прочность в онлайн-калькуляторе или вручную следует уменьшать сечение только до тех пределов прогиба, которые меньше вычисленного значения.

На иллюстрации выше показана расчетная схема для распределенной нагрузки, то есть такой, которая равномерно распределяется по всей балке. Обычно в жилых помещениях используется именно эта схема. Однако при размещении в комнате мебели или оборудования большого веса, особенно не возле стены (на которую опирается край балки), а на некотором удалении от нее, иногда бывает разумнее использовать схему расчета для сосредоточенной нагрузки.

Вот так примерно создается сосредоточенная нагрузка на балку.

Таблица 1.2. Схемы расчета деревянных балок с одной сосредоточенной нагрузкой.

Здесь и далее Е – модуль упругости древесины Е=100 000 кгс/м2), I – осевой момент инерции балки.

Таблица 1.3. Схемы расчета деревянных балок с двумя сосредоточенными нагрузками.

Таблица 1.4. Расчет балки с двусторонним жестким защемлением при равномерно-распределенной нагрузке.

В зависимости от того, куда именно приложены нагрузки и в каком количестве, используется расчетная схема соответствующего типа.

Для бруса, защемленного в стене только одним концом (консольное крепление), используются другие формулы расчета деревянной балки на прочность. Обычно такие вычисления нужны при проектировании навесов на деревянных балках-опорах, больших вылетов крыши и других подобных случаях.

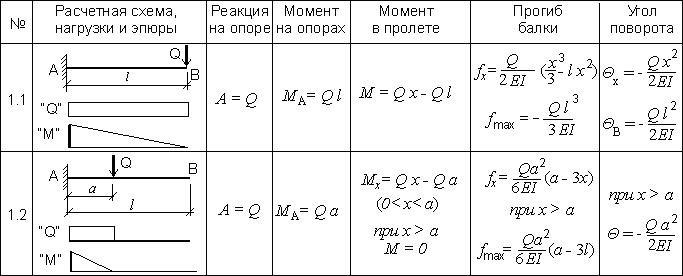
Таблица 1.5. Расчет консольной балки при одной сосредоточенной нагрузке.

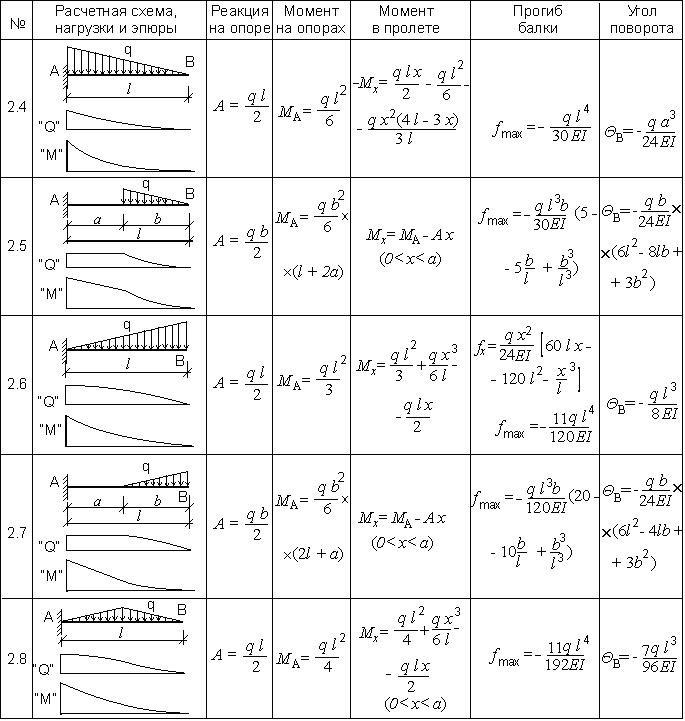
Таблица 1.6. Расчет консольной балки при одной неравномерно-распределенной нагрузке.

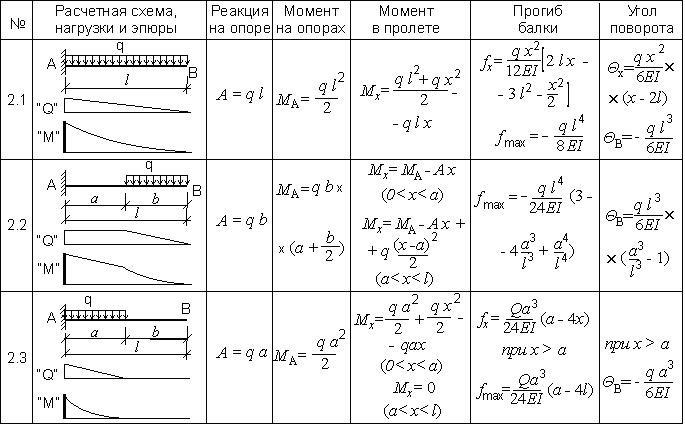
Таблица 1.7. Расчет консольной балки при одной равномерно-распределенной нагрузке.

Формулы кажутся громоздкими и сложными, но фактически обычному пользователю при расчете деревянных балок перекрытия важно просто представлять себе характер распределения действующих на балку сил и понимать – чтобы соблюсти условия прочности, необходимо правильно выбрать схему приложения нагрузок

Пример расчета прогиба балки

Для закрепления пройденного материала, предлагаю рассмотреть пример с заданными численными значениями всех параметров балки и нагрузок. Возьмем также консольную балку, которая жестко закреплена с правого торца. Будем считать, что балка изготовлена из стали (модуль упругости E = 2·105 МПа), в сечении у нее двутавр №16 (момент инерции по сортаменту I = 873 см4). Рассчитывать будем прогиб свободного торца, находящегося слева.

Подготовительный этап

Проводим подготовительные действия, перед расчетом прогиба: помечаем базу O, с левого торца балки, проводим координатные оси и показываем реакции, возникающие в заделке, под действием заданной нагрузки:

В методе начальных параметров, есть еще одна особенность, которая касается распределенной нагрузки. Если на балку действует распределенная нагрузка, то ее конец, обязательно должен находиться на краю балки (в точке наиболее удаленной от заданной базы). Только в таком случае, рассматриваемый метод будет работать. В нашем примере, нагрузка, как видно, начинается на расстоянии 2 м. от базы и заканчивается на 4 м. В таком случае, нагрузка продлевается до конца балки, а искусственное продление компенсируется дополнительной, противоположно-направленной нагрузкой. Тем самым, в расчете прогибов будет уже учитываться 2 распределенные нагрузки: