Площадь треугольника

Как рассчитать площадь комнаты стандартной формы

Под площадью комнаты подразумеваются числовые характеристики, которые показывают её размер в двухмерном пространстве. Если комната стандартная (прямоугольная или квадратная), то сделать расчёт легко. Нужно только померить длину и ширину. Делается это вдоль стен по полу, при загроможденности данных участков, возможно, проводить замер посредине комнаты.

Важно, одна сторона должна измеряться строго перпендикулярно второй. Стороны расположенные параллельно должны иметь один размер, но несмотря на это, меряются обе

Кроме того, следует проверить правильность формы, то есть провести промеры диагоналей. В прямоугольном или квадратном помещении, они должны равняться, или иметь небольшие отклонения.

Квадратное помещение

Как рассчитать S квадратных помещений — это довольно легко. У квадратной комнаты все стороны равны.  Однако, как говорилось выше, надо замерить их все, и взять средне арифметический показатель для расчёта:

А — размер сторон.

Рассмотрим пример: комната со стенами по 3 метра, 3 в квадрате — S = 9 м2.

Прямоугольное

Рассчитать площадь помещений прямоугольной конфигурации, также легко путём следующих вычислений:

На примере видно, при ширине 4,10 м, длине 6,15 м, S комнаты получается — 4,10 x 6,15 = 25,215 м2. После запятой оставляется две цифры, остальные округляются, то есть выходит 25,22 м2.

Как рассчитать площадь?

Площадь треугольников всегда рассчитывается по одной и той же формуле, умножая основание на высоту и деля на два:

Площадь = (база _* ч) ÷ 2

В некоторых случаях высота разностороннего треугольника неизвестна, но есть математическая формула, предложенная математиком Хероном, для расчета площади, зная измерение трех сторон треугольника..

где:

• a, b и c, представляют стороны треугольника.
• sp, соответствует полупериметру треугольника, то есть половине периметра:

sp = (a + b + c) ÷ 2

В случае, если у вас есть измерение только двух сторон треугольника и угла, который сформирован между ними, площадь может быть рассчитана путем применения тригонометрических соотношений. Итак, вы должны:

Площадь = (сторона _* ч) ÷ 2

Где высота (h) — произведение одной стороны на синус противоположного угла. Например, для каждой стороны площадь будет:

• Площадь = (б _* с _* сен а) ÷ 2
• Площадь = (а _* с _* сен Б) ÷ 2.
• Площадь = (а _* б _* сен C) ÷ 2

Особенности фронтонов и способы расчета их площади

Разберем все аспекты, связанные с данной частью конструкции, чтобы вы разобрались в теме досконально и смогли все рассчитать самостоятельно.

Типы конструкций по способу монтажа

Есть два основных варианта, которые очень сильно отличаются друг от друга, разберем каждый из них более подробно.

Первый тип сооружается еще до монтажа кровли, его основные особенности таковы:

От фронтона зависит вся кровля. Конструкция обычно выполняет роль несущего элемента, определяющего размер и конфигурацию будущей крыши

В этой ситуации очень важно правильно произвести все расчеты. Любые ошибки чреваты искривлением скатов, которые вряд ли удастся устранить без демонтажа всей кровельной конструкции;

Фронтон дома из бруса

Чаще всего такие элементы служат продолжением стены и создают сплошную поверхность от верха до низа. Это позволяет получить прочную конструкцию, которая будет выдерживать высокие нагрузки. Такой способ сооружения коробки позволяет сэкономить время и деньги;

Фронтон из блоков

Фронтоны могут иметь окна, если сооружается дом с жилым мансардным этажом. Это существенно усложняет рабочий процесс, поэтому сооружение таких вариантов лучше поручить профессионалам;

Окна под будущее жилое помещение

Второй вариант ставится после сооружения стропильной системы, это более простое решение, имеющее такие особенности:

Для укрепления поверхности в первую очередь ставится каркас. Он должен быть достаточно надежным, чтобы обеспечивать дополнительную опору кровельной системе, тем самым повышая ее устойчивость к ветровым и снеговым нагрузкам;

Каркас фронтона двухскатной крыши неправильной формы

• Это более простой вариант, так как вам не нужно рассчитывать конфигурацию конструкции. Поэтому данное решение более предпочтительно для тех, кто не имеет опыта работ;
• Для сооружения можно использовать не такой материал, как для стен. Да и поверхность фронтона может быть несколько выдвинута относительно поверхности стены.

Материал отделки фронтона может отличаться от того, что использовано на стенах

Расчетные работы

Даже если вы будете использовать онлайн-калькулятор, вам нужно знать несколько цифр:

Иллюстрация	Описание
	Высота. Это расстояние от основания конструкции до ее самой верхней части. Этот показатель можно найти и в проектной документации, но лучше дополнительно перепроверить его лично.
	Ширина фронтона. Это расстояние по основанию конструкции — в самой широкой части. На схеме показаны два самых распространенных варианта и указано, в каких местах нужно определять длину и ширину.
	Определение угла ската кровли. Если у вас нет оборудования для определения этого показателя — не беда. Воспользуйтесь таблицей слева. Для этого отмеряйте ровно 1 метр от края фронтона, после чего измерьте высоту ската в этом месте. Полученное значение подскажет вам уклон.
	Площадь треугольника фронтона вычисляется так: высота конструкции умножается на ширину и делится на 2. Так мы получаем квадратуру элемента и можем определить, сколько материалов для его отделки и утепления потребуется. Если скаты несимметричные, то рассчитайте площадь каждой половинки отдельно и суммируйте результат.
	Площадь трапециевидного фронтона определяется так: высоту нужно умножить на среднюю линию (средняя линия — это половина суммы длин верхнего и нижнего основания). Далее вам надо вычислить площадь треугольной обрасти наверху так, как описано выше, цифры суммируются, и вы получаете точную площадь конструкции.

Площадь квартиры

Так как ремонт — это «бедствие», которое периодически нас посещает, лучше сделать план всей квартиры с подробными замерами. На этом же плане проставьте площади каждого помещения. После того, как рассчитаете квадратуру всех комнат, сложите цифры и получите метраж квартиры.

Для плана лучше рассчитать метраж каждой комнаты

Один вариант может быть как на рисунке выше — для того, чтобы знать именно площади каждого помещения. Это потребуется для закупки материалов. Но нужен будет еще план, на котором будут все длины. Простенки, ширина окон, дверей и т.д. Это потребуется, например, для разработки схем укладки ламината, напольной плитки или других покрытий. Нужен будет такой план и при планировании теплого пола.

Есть, кстати, приложение-калькулятор для телефона, при помощи которого все вычисления сделать очень просто.

Какие инструменты применяют для расчета площадей?

Для расчета площади комнаты можно использовать различные компьютерные программы, также применяются различные математические формулы для вычислений. Но размеры сторон геометрической фигуры, которой соответствует помещение, снимать придется в любом случае.

Таблица. Инструменты для снятия размеров комнаты.

Наименование	Рекомендации
Бумага и ручка/карандаш	Необходимы для записи полученных показаний. Если показания не записывать, то можно быстро запутаться. Также бумага и пишущие принадлежности пригодятся для составления плана помещения.
Рулетка	С ее помощью и определяются непосредственно все размеры. Чем больше комната, тем длиннее рулетку придется приобрести. Не стоит использовать мягкую тканевую сантиметровую ленту, которой пользуются закройщики – она достаточно короткая и мягкая, потому снимать мерки будет неудобно и можно допустить погрешности.
Калькулятор	Необходим для совершения всех математических операций. Удобен тем, что позволит снизить риск возникновения погрешностей.
Лазерный дальномер	Удобный прибор, который позволит быстро и точно снять мерки любого помещения.
Угольник, транспортир	Может понадобиться для измерения углов в помещении. Стоит помнить, что даже кажущиеся прямыми углы не всегда бывают такими. А порой знать точный размер угла необходимо.

Расчет вручную на листочке удобен тем, что все параметры можно тут же перемерить на месте и внести необходимые коррективы. Но ошибиться при ручном способе расчетов довольно просто, поэтому лучше лишний раз пересчитать все показатели.

Для автоматического подсчета площади помещения удобно использовать различные графические редакторы. Это могут быть AutoCAD, ArchiCAD или SketchUP. В них создается фигура по форме комнаты, размеры всех ее сторон указываются при создании макета. Площадь комнаты будет выдана программой автоматически и с высокой точностью (вплоть до сантиметров и миллиметров). Все будет зависеть от точности снятых мерок. Особенно использование этих программ рекомендуется, если необходимо высчитать площадь комнаты, сложной по своей геометрии. Недостатком этого метода является необходимость хотя бы поверхностного изучения программ, а также использование компьютерной техники.

Пример использования программы SketchUP

Площадь треугольника | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU

Площадь любого треугольника можно найти, зная основание и высоту. Вся простота схемы заключается в том, что высота делит основание a на две части a

1 и a₂, а сам треугольник – на два прямоугольных треугольника, площадь которых получается и . Тогда площадь всего треугольника будет суммой двух указанных площадей, и если мы вынесем одну вторую высоты за скобку, то в сумме мы получим обратно основание:

Более сложный для расчетов способ – это формула Герона, для которой необходимо знать все три стороны. Для этой формулы нужно вычислить сначала полупериметр треугольника:
Сама формула Герона подразумевает квадратный корень из полупериметра, умноженного поочередно на разность его с каждой из сторон.

Следующий способ, также актуальный для любого треугольника, позволяет найти площадь треугольника через две стороны и угол между ними. Доказательство этому проистекает из формулы с высотой – проводим высоту на любую из известных сторон и через синус угла α получаем, что h=a⋅sinα . Для вычисления площади умножим половину высоты на вторую сторону.

Другой способ – найти площадь треугольника, зная 2 угла и сторону между ними. Доказательство этой формулы достаточно простое, и наглядно видно из схемы.

Опускаем из вершины третьего угла высоту на известную сторону и называем полученные отрезки x соответственно. Из прямоугольных треугольников видно, что первый отрезок x равен произведению котангенса угла α на высоту, а второй отрезок y – произведению котангенса угла β на эту же высоту. Дальше соединяем это вместе:

Инструментальные обмеры дома

Для измерения площади дома потребуются инструменты, чтобы очень точно выполнить расчеты, которые могут стать основой для проведения ремонтных работ, купли-продажи или страхования дома. Перед тем как рассчитать площадь, нужно взять рулетку, карандаш и блокнот, на котором нарисовать простейшую схему плана дома. Ее можно взять из паспорта застройщика или других проектных документов. С последним источником нужно быть внимательным, указанные цифры могут быть не всегда точными, например, какие-то ремонтные работы могут быть в них не учтены. Поэтому правильнее будет выполнить измерение площади самостоятельно.

Как рассчитать площадь дома вручную? Если нужно измерять площадь пола вручную, лучше всего измерить внешние стены, не забывая различных строительных углублений, подсобных помещений, верхних этажей, отдельных зданий или гаражей. Когда сделаны простые основные измерения, площадь рассчитывается путем умножения длины дома на ширину.

В зависимости от формы плана строительства может понадобится разбить его на простейшие геометрические фигуры. В этом примере дом имеет 9 метров на 12 метров, давая нам 108 квадратных метров. Гараж составляет 6 метров на 3 метра, что составляет 18 квадратных метров, общая площадь – 126 квадратных метров.

Объем комнаты

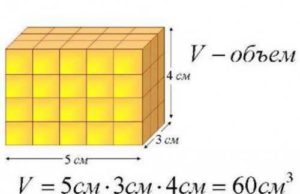
Формула расчета объема комнаты

Для некоторых расчетов требуется объем комнаты. В этом случае перемножаются три величины: ширина, длинна и высота помещения. Измеряется данная величина в кубических метрах (кубометрах), называется еще кубатурой. Для примера используем данные из предыдущего пункта:

Если все перемножить, получаем: 5,6 м * 3,2 м * 2,5 м = 44,8 м 3. Итак, объем помещения 44,8 куба.

PropertyExperts Портал Экспертов по Недвижимости

Если вы собрались делать ремонт, первое, что вам необходимо сделать, это спланировать бюджет ремонтных работ, а для этого, в свою очередь необходимо знать, сколько понадобится строительных и отделочных материалов, при условии, конечно, что вы уже определились с дизайн-проектом и точно знаете, где будет установлена плитка, какие стены «пойдут под покраску» или фактурную штукатурка, и где будет находится встроенный шкаф.

Интересуясь стоимостью услуг на ремонтные работы, вы обратите внимание на то, что все цены, как правило «привязаны» к квадратным метрам. Собственно и бюджет ремонта квартиры напрямую связан с площадью ваших квадратных метров

Вот мы и подошли к главному вопросу нашей статьи — как посчитать квадратные метры?

Посмотрите внимательно на свою комнату. Комната состоит из стен, пола и потолка, в ней имеются также окна и двери. Вот вам и понадобится вычислить площадь всех поверхностей, которые будут подвержены ремонтным работам, с учетом всех дополнительных составляющих, каковыми являются окна и двери.

Для того, чтобы понять, как рассчитать квадратные метры комнаты. необходимо вспомнить средний курс школьной математики, а именно как вычисляется площадь поверхности.

Каждая из стен, а также потолок и пол представляют собой либо квадрат, либо прямоугольник. Стены имеют ширину и высоту, пол и потолок имеют длину и ширину, измеряемые в метрах. Как вычислить квадратный метр ?

Итак, площадь прямоугольной или квадратной поверхности высчитывается по формуле:

а и в — стороны прямоугольника (стен, потолка, пола).

Приведем конкретный пример, как рассчитать метр квадратный :

Предположим, длина вашей комнаты 6 метров, а ширина — 4 метра, тогда:

площадь комнаты по полу будет равна 24 квадратных метра:

Теперь посчитаем площадь комнат по стенам. Предположим высота потолков у вас — 3 метра, тогда:

площадь комнаты по одной стене будет равна 18 квадратным метрам

площадь комнаты по другой стене будет равна 12 квадратным метрам

площадь четырех стен равна 60 квадратным метрам

Как считать квадратные метры. вы уже знаете. Но для ремонта и точного расчета площади, например штукатурных работ, вам необходимо вычислить из общей площади стен площади, которые занимают окна и двери. Ведь их штукатурить или шпатлевать не надо.

Аналогично вычисляете площадь прямоугольника, который занимают окна и двери. Предположим высота двери 2 метра, а ширина 0,90 м, тогда:

площадь дверного полотна равна 1,8 метра квадратных

Считаем площадь, которую занимает оконный проем. Если высота окна, допустим, 1,5 метра, а ширина 1,6 метра, то:

площадь окна в нашем примере равна 2,4 квадратных метра

Если в комнате одна дверь и одно окно, то из общей площади стен необходимо вычесть площадь, которую занимают окна и двери:

Итак, общая площадь стен 55,8 квадратных метров, площадь пола и потолка по 24 квадратных метра.

Игорь Воропаев — ведущий юрист «Проспер-Консалтинг» Консультант портала PropertyExperts

Я несколько лет работаю в строительной фирме и практически ежедневно выезжаю на измерения размеров помещений. Каждому, кто планирует воспользоваться услугами нашей фирмы, перед началом работ обязательно необходимо вызвать специалиста и замерить геометрический периметр, определить фигуру комнаты (может быть даже треугольник), количество простых и сложных форм (выступов, ниш), а также определить значения прочих величин в кубических и погонных метрах.

Если это внешняя отделка, также измеряется крыша и вся конструкция. Также приезжает ученик, который проводит вычисления (может потребоваться несколько минут, т.к. необходимо умножить обмеры). Произведя перевод показателей и единиц, он представит быстрый итоговый результат с наличием правильных размеров, по которым будет рассчитываться расход на проведение различных работ (количество рулонов бумаги, вагонки, покрытия в ванную, вес шпаклевки).

На основании этих данных и будет задаваться общая стоимость работ. Мы не берем оплату за эти работы, если ремонт заказывается у нас. Именно в таком случае исключается то, что будут возникать проблемы по материалам или объему работ, что удобно всем.

Различные типы треугольников в зависимости от длины их сторон

Разносторонний треугольник

Мы узнаем разносторонний треугольник по трем сторонам, которые имеют разную длину. Эта треугольная форма может быть построена только с тремя разными углами. Кроме того, один из них может быть прямым углом (или углом 90 °). В общем, название «произвольный треугольник» используется для разностороннего треугольника.

Равнобедренный треугольник

Мы говорим, что треугольник равнобедренный, если он имеет две стороны одинаковой длины и два равных угла при основании. Равнобедренный треугольник также можно узнать по тому факту, что его высота представляет его ось симметрии, его медиану и биссектрису.

Прямоугольный треугольник

Прямоугольный треугольник обязательно имеет прямой угол. Другими словами, сумма двух других его углов должна быть равна 90°. Прямоугольный треугольник также имеет гипотенузу.

Это противоположная сторона вершине с прямым углом. Прямой треугольник может быть разносторонним (или любым), если его три стороны имеют разную длину.

Кроме того, он может быть равнобедренным в том случае, если он имеет два одинаковых катета.

Равносторонний треугольник

Треугольник называется равносторонним, если он имеет три стороны одинаковой длины. Поэтому все его углы также равны и каждый по 60°. В равностороннем треугольнике любая высота также выступает в качестве медианы и биссектрисы.

Площадь равностороннего треугольника по радиусу описанной окружности

Пусть в прямоугольном треугольнике известна радиус описанной окружности R (Рис.3):

Найдем площадь равностороннего треугольника. На рисунке 3 равносторонний треугольник разделен на 6 частей. Полученные 6 прямоугольные треугольники равны по катету и гипотенузе. Тогда:

Чтобы найти площадь треугольника ABC достаточно найти площадь одного из прямоугольных треугольников и умножить на 6.

Применим для треугольника OBE теорему синусов:

Еще раз применим теорему синусов для треугольника OBE :

Подставляя (11) и (12) в (10), получим:

Наконец, площадь треугольника ABC равна:

Пример 4. Радиус oписанной окружности равностороннего треугольника равна R=11.2. Найти площадь треугольника.

Решение. Для вычисления площади треугольника воспользуемся формулой (14). Подставляя значение R=11.2 в (14), получим:

Ответ:

Зачем проводить расчет площади комнаты?

Любой ремонт не может начинаться без точных знаний о размерах комнаты. Чтобы посчитать количество обоев или панелей, нужно узнать размеры и площадь стен, для приобретения достаточного количества потолочной плитки снимаются мерки с потолка. Конечно, для закупки в требуемых объемах напольного покрытия также придется постараться и узнать значение площади всего пространства пола.

Для чего могут пригодится расчеты площади

Со снятием мерок с помещения и определением площади основания сталкивается каждый человек, который решил самостоятельно начать ремонт. Если владелец жилого помещения обратился за помощь к специалистам, то ему ни во что вникать не придется – мастера все сделают сами. Однако все же многие решаются на проведение ремонтных работ своими руками. Это позволяет значительно сэкономить деньги, затраченные на ремонт.

Для ремонта необходимо точно знать размеры комнаты

Основные причины необходимости определения площади пола следующие:

• ремонт или первичная укладка напольного покрытия;
• заливка свежей стяжки;
• обустройство системы лаг;
• окрашивание пола;
• нанесение на пол других строительных материалов;
• определение размера жилой площади при оформлении документов либо покупке/продаже квартиры или дома;
• определение соответствия помещения плану комнат;
• подбор мебели по габаритам;
• составление плана комнаты для проведения дальнейших работ;
• оценка стоимости работы специалистов и других затрат.

Не всегда измерение площади пола оказывается простой процедурой

В основном, знание площади пола требуется для того, чтобы высчитать нужное для отделки количество строительных материалов, которые будут использованы при работе. Например, объем цементной смеси для заливки стяжки, количество наливного пола или пачек ламината и т. д.

Виды напольного покрытия

Пол оригинальной формы

Первое, что следует сделать при подсчёте площади пола неправильной формы — мысленно или на бумаге расчленить его на простые фигуры. После чего высчитать отдельно площадь каждой из них и суммировать результаты.

По ходу выполнения этого задания вы обязательно заметите, что фигуры сами по себе простые, а вот процесс вычисления их площади не всегда. Для каждой отдельной части придётся применять свою формулу в зависимости от её геометрии. Некоторые из них мы сейчас рассмотрим.

Треугольники

Проще всего иметь дело с прямоугольными представителями этого семейства. Начертив его на бумаге, несложно заметить, что он составляет половину прямоугольника. Соответственно и формула расчёта отличается незначительно: S=a*b/2. Где под буквами a и b подразумевается длина катетов (сторон, соприкасающихся под прямым углом).

Если треугольник не имеет прямых углов, необходимо провести следующие действия:

• принять одну из его сторон за основание;
• провести от вершины к нему высоту;
• умножить одно на другое;
• результат разделить на 2.

В итоге формула будет иметь такой вид: S=a*h/2. Где a и h — длина основания и высота соответственно.

Для любителей экзотики существуют и другие варианты. Например, формула Герона, или подсчёт с помощью радиуса вписанной в треугольник окружности. Но проще всё-таки будет считать через основание и высоту.

Круги и овалы

Такие геометрические формы в строительстве встречаются редко, но всё же встречаются. Чтобы рассчитать площадь круга достаточно найти его радиус и подставить в уравнение: S=πr2. Оно известно нам ещё со школы. И, если верить учебникам, r — это радиус круга, а величина π равна 3,14.

Площадь овала (эллипса) вычисляется похожим образом. Только вместо радиуса необходимо найти длину двух его полуосей — длинной (a) и короткой (b). Дальше — по той же схеме: S=π*a*b.

Но чаще можно столкнуться с полукруглыми или «полуовальными» помещениями. Для подсчёта размеров такой комнаты к формулам для круга и овала в конце дописываем /2. На латыни это будет выглядеть так: S=πr2/2 и S=π*a*b/2.

Многоуровневый пол

Встречается ещё реже. И посчитать его площадь можно так, как и в примере с прилегающими помещениями — сложить показатели каждого фрагмента. Но, если вам нужно такой пол покрасить, то не забудьте учесть и вертикальные плоскости. В противном случае краски на них может не хватить.

В конце хотелось бы отметить, что главное в любых расчётах — точность. Поэтому будьте внимательны при выполнении замеров и тщательно проверяйте результаты вычислений. Это значительно упростит дальнейшие, более сложные действия во время ремонта.

Площадь треугольника — калькуляторы для всех видов

Треугольники бывают остроугольными, тупоугольными, прямоугольными, разносторонними, равносторонними, равнобедренными. Рассмотренные в данном пункте калькуляторы и формулы подходят для всех видов треугольников.

Зная сторону треугольника (основание) и высоту проведенную к основанию, можно найти его площадь. Площадь треугольника будет равна половине произведения основания на высоту. Основанием треугольника может быть выбрана любая из сторон треугольника.

Площадь треугольника по основанию и высоте — калькулятор онлайн:

Формула	Результат
S = ½ × a × h
	Сторона a
Высота h

Если известно две стороны треугольника и угол между ними, то площадь данного треугольника вычисляется, как половина произведения этих сторон умноженная на синус угла между ними. Угол α между сторонами может быть любым: тупым, острым, прямым.

Площадь треугольника по двум сторонам и углу между ними — расчет:

Формула	Результат
S = ½ × a × b × α
	Сторона a
Сторона b
Угол α° между сторонами a и b

Если известно три стороны треугольника и радиус вписанной окружности, то площадь данного треугольника вычисляется, как половина суммы этих сторон (полупериметр p = ½ × (a + b + c)) умноженная на радиус вписанной окружности.

Площадь треугольника по радиусу вписанной окружности и трем сторонам — онлайн калькулятор:

Формула	Результат
S = r × ½ × (a + b + c)
	Сторона a
Сторона b
Сторона c
Радиус r вписанной окружности

Если известно три стороны треугольника и радиус описанной окружности, то площадь треугольника равна частному от деления произведения сторон треугольника на четыре радиуса описанной около треугольника окружности.

Площадь треугольника по радиусу описанной окружности и трем сторонам — расчет:

Формула	Результат
S = (a × b × c) ⁄ (4 × R)
	Сторона a
Сторона b
Сторона c
Радиус R описанной окружности

Площадь треугольника по формуле Герона равна корню из произведения разностей полупериметра треугольника (p) и каждой из его сторон (a, b, c) на полупериметр. Полупериметр p = (a + b + c) × ½.

Площадь треугольника по формуле Герона — калькулятор онлайн:

Формула	Результат
S = √ p × (p — a) × (p — b) × (p — c)
	Сторона a
Сторона b
Сторона c

Площадь произвольного треугольника по стороне и двум прилежащим углам — расчет:

Формула	Результат
S = ½ × a² × (sin α × sin β) ⁄ sin (180 — (α + β))
	Сторона a
Угол β°
Угол α°

Способы нахождения площади

Но существуют также и другие способы, по которым можно найти S этого многоугольника. Рассмотрим основные из них.

Через две стороны и угол

Если вам известны две стороны любого треугольника и угол между ними, найти площадь можно по формуле:

\(S=\frac12a\times b\times\sin\alpha\)

где a и b — стороны фигуры, а α — угол между ними.

Через радиус описанной окружности и три стороны

Если вам известен радиус окружности, которая описана вокруг вашего треугольника, а также все его стороны, можно вычислить S следующим образом:

\(S=\frac{a\times b\times c}{4\times R}\)

где a, b и c — стороны фигуры, а R — радиус описанной окружности.

Через радиус вписанной окружности и три стороны

В случае, если вам известны все три стороны и радиус вписанной в треугольник окружности, можно найти его площадь по формуле:

\(S=r\times\frac{a+b+c}2\)

где r — радиус вписанной окружности, \(\frac{a+b+c}2\) — полупериметр фигуры.

Таким образом, формулу можно выразить всего двумя множителями:

\(S=r\times p\)

где p — полупериметр треугольника.

Через сторону и два угла

Если в данной фигуры вам известна лишь одна сторона и две прилегающих к ней угла, ее S можно найти следующим образом:

\(S=\frac12\times a^2\times\frac{\sin\alpha\times\sin\beta}{\sin\gamma}\)

причем \(\gamma=180^\circ-(\alpha+\beta)\)

Геометрия фронтона и методика вычислений

Пространство под крышей выполняет несколько функций: укрепляет, утепляет и защищает крышу; оно облицовывается подходящим материалом, поэтому для закупки отделки важно знать его размеры. Вид и материал фронтона определяется технологией строительства дома, при этом возможно два варианта его обустройства:

• Как продолжение несущей внешней стены. Его изготавливают из того же материала, что и стены. 
• Как отдельная конструкция. Для его обустройства применяют каркас из бруса или металлических опор, который затем обшивают.

Фронтальная часть стандартной двускатной кровли имеет вид симметричного (равнобедренного) треугольника. Если дом спроектирован с мансардной крышей, то вместо треугольника получается более сложная фигура (так как у мансарды имеются стены). Ее можно представить в виде суммы двух фигур: треугольника и трапеции.

Реже проектируются несимметричные кровли; у них боковая плоскость также получается несимметричной, и определение площади фронтона несколько усложняется. Нетривиальные варианты (полукруглый, ступенчатый) в частном домостроении практически не встречается. Исходя из конструктивных особенностей кровли, я выбираю одну из двух методик:

Простая форма, треугольник или трапеция. Вы можете приступать непосредственно к расчетам, без предварительной подготовки. 
Сложная форма, характерная для мансардной или ломаной кровли с несколькими углами наклона скатов

Здесь важно правильно представить фигуру в виде более простых элементов.

Разбивку удобно делать при помощи одной горизонтальной линии, но для усложненных и несимметричных конструкций может потребоваться несколько дополнительных линий, и не только горизонтальных, но и вертикальных. В результате разбивки у вас должен получиться набор элементарных фигур, треугольников, прямоугольников, трапеций. Идея состоит в определении площади каждой из этих фигур с дальнейшим сложением результатов.

Как подготовиться к расчетам

Проведение подготовительных манипуляций заключается в подготовке места для измерений. Также необходимо подготовить инструмент и специальные принадлежности. Лучше если комната будет свободной от посторонних предметов. Часто такое случается при замерах в новом доме или во время проведения ремонта. Замеры длины сторон производятся вдоль стенок. При этом нужно освободить хотя-бы участки, для свободного проведения рулеткой. Результаты замеров можно сразу же перенести на схему. Обязательно следует проверить прямоугольности комнаты. Для этого выполняется замер диагональных линий.

Особенности замеров с учетом линий коммуникаций

Кроме рулетки вам может понадобиться специальная линейка для проверки прямых линий. Это может быть строительный уровень или правило. Иногда необходим строительный угольник больших размеров. Как вариант, самодельный циркуль. Можно использовать кусок шнура, привязанный к острому штырю. Для пола можно использовать специальные принадлежности для замеров. Для этого подойдет маркер, мел или скотч. Замеры выполняйте несколько раз. Это позволит избежать ошибки. Следите, чтобы лента для проведения замеров не провисала. Помните, что на многие измерительные инструменты наносится две шкалы. Нельзя путать метрическую систему и дюймовую.

Лазерное приспособление заметно облегчает работу

Перед замерами набросайте простой план – схему на бумаге. Это позволит правильно распределить все замеры. Стоит учитывать, что многие формулы расчетов очень сложные. В этом случае посчитать в столбик не получится. Чтобы посчитать без ошибок, можно воспользоваться программой Excel.

На схеме показаны все необходимые замеры для правильных расчетов

Считаем количество плитки

Зная площадь комнаты, рассчитать количество напольного покрытия будет несложно. Разберемся, как выяснить, сколько плитки понадобится для конкретной комнаты. Для этого нужно узнать, какова площадь одного элемента плиточного покрытия. Зная эти данные, легко произвести необходимые расчеты. Например:

• площадь комнаты – 15 м2;
• размер одной единицы плитки – 0,20х0,30 м.

Расчет количества плитки на пол

Таким образом, площадь одной плитки составит 0,2х0,3 = 0,06 м2. Далее общую площадь комнаты делим на площадь одной плитки и получаем: 15/0,06 = 250 единиц. Именно столько плиток потребуется, чтобы закрыть весь черновой пол в данном помещении. Точно таким же методом вычисляется и количество ламината или паркетной доски, а также других материалов.

Видео – Рассчитываем линолеум

Чтобы высчитать площадь пола в комнате, а затем – и расход материала, достаточно знать элементарные математические формулы и уметь пользоваться калькулятором. Имея последний под рукой (а сейчас калькулятор есть в каждом телефоне), произвести расчеты можно быстро. Главное – быть внимательными при снятии замеров.

Площадь равносторонних треугольников — онлайн калькулятор, формулы

Правильный (равносторонний, или равноугольный) треугольник — это правильный многоугольник, все стороны которого равны между собой, все углы также равны и составляют 60°. В равностороннем треугольнике высота является и биссектрисой, и медианой.

Площадь равностороннего треугольника по известной стороне равна произведению одной четвертой корня из трех на квадрат стороны.

Площадь равностороннего треугольника по стороне — онлайн расчет:

Формула	Результат
S = ¼ × √(3) × a²
	Сторона a (a = b = c)

Если известна высота равностороннего треугольника, то его площадь равна отношению квадрата высоты к корню из трех.

Площадь равностороннего треугольника по высоте:

Формула	Результат
S = h² ⁄ √(3)
	Высота h

Если известен радиус вписанной окружности, то площадь равностороннего треугольника равна произведению трех корней из трех на квадрат радиуса вписанной окружности.

Площадь равностороннего треугольника по радиусу вписанной окружности — калькулятор:

Формула	Результат
S = 3 × √(3) × r²
	Радиус r вписанной окружности

По известному радиусу описанной окружности площадь равностороннего треугольника определяется, как произведение трех четвертей корня из трех на квадрат радиуса.

Площадь равностороннего треугольника по радиусу описанной окружности:

Формула	Результат
S = ¾ × √(3) × R²
	Радиус R описанной окружности